ADRC课程笔记

本人对ADRC控制有着深厚的研究兴趣。在讨论研究韩京清先生的ADRC知识之前，我想先给不太专业的自己补习一些经典与现代控制理论方向的相关知识。

生理前馈系统

在生理学上，前馈控制的例子是在实际体力活动之前，自主神经系统对心跳的正常预期调节。前馈控制可以比作对已知线索的预期反应（预测编码）。心跳的反馈调节为机体提供了进一步对运动的适应性。 –wiki百科

在前馈系统中，控制变量的调整不是以目标和回授之间的误差为基础，它是以过程数学模型的知识和过程扰动的知识或测量为基础。

所以对于数学模型的整体掌握是对系统扰动进行前馈消除的前提。

正所谓要想系统稳得住，必须得有前馈引入。前馈控制在某些控制场合下是必须项。

前馈控制

摘自《高志强: 自抗扰控制思想探究》

前馈控制是一种基于对扰动的预测进行补偿的控制方法。它通过测量可能影响系统输出的扰动变量，并根据扰动变量与系统输出之间的关系，计算出所需的控制量，在扰动对系统产生影响之前就进行调节，以抵消扰动的影响。
在自动控制系统理论中学习过，由传递函数理论数学推导，前馈的引入可以完全的消除系统的扰动误差。现在这显然并不是这么的简单，这需要对系统数学模型有着十分精确的掌握。
前馈控制在工业界用途广泛, 但是学术界对它很少关心, 认为是开环控制, 没有什么理论可言. 前馈的使用方式主要有两种: 一种是根据参考输入和对象模型的逆而得到的控制量, 不依赖对象的实时信息,暂且称之为A类前馈; 另外一种前馈, 是根据被控量之外的对象信息所产生的控制量, 即B类前馈。
前馈控制提出的本意是要区别于上面提到的狭义的反馈控制, 表示控制量的一部分甚至全部都可以完全独立于被控量的量测. Black定义的反馈(feedback)本来就是针对前馈(feedforward)而言的, 表示信号流向反转, 由输出到输入. 这里信号的走向一正一反, 概念很清楚。
可是当反馈这个通讯工程的概念被借用到控制工程时, 它的反义词前馈的含义便有了两种解释. 比如上面说的A类前馈明显是开环控制, 控制量完全独立于对象的实时信息. 可是B类前馈则不然, 它依赖的还是对象信息, 实际上是前面提到的广义反馈, 只不过反馈的不是输出量而已. B类前馈在文献中也被称为扰动前馈, 它是基于对象扰动信息的实时提取, 就像指南车. 可是同样是基于对象信息的提取, 指南车为什么会被称为开环控制呢？其实B类前馈属于广义反馈, 不应称其为前馈或开环控制. 鉴于前馈的概念和用法前后重叠, 为了概念的清晰, 建议今后可把B类前馈归入抗扰原理讨论; 把前馈狭义地定义为A类前馈.那么这样的前馈有什么意义呢？为什么它的用途这么广呢？主要原因是它降低了快速跟踪的成本。
一个控制系统要使输出迅速跟踪给定值有两个途径: 1) 高带宽; 2) 前馈. 但是在工业上, 带宽就是成本.高带宽虽然能使跟踪速度提高, 但也带来很多问题:1) 对执行机构的品质要求提高; 2) 激励了对象的高频动态使控制问题复杂化; 3) 闭环系统的稳定裕度下降,对相位滞后和时间延迟更敏感; 4) 对传感器噪声更敏感, 等等.高带宽的成本在20世 50年代就有专门、详细的讨论, 比如文献[46], 但是至今没能在理论界引起重视, 乃至高增益控制器、观测器的文章比比皆是, 而能用上的却寥寥无几. 这反映了不考虑成本的研究, 在工程上是没有多少意义的。
工程师们在实践中基于对系统物理特性的知识发现了前馈这个办法. 这种独立于反馈回路拟合出的控制量通常是结合参考输入, 以数据或图表形式表示的,常常在控制信号中占主要部分. 同时也使用PID反馈控制器, 发挥微调、纠错的作用. 因此, 工业上的PID控制器常常是与前馈控制结合使用的。
以上总结的是控制论的基本原理, 是从事自动控制的人们在长期的工程实践中发现、挖掘出来的, 是控制论继续发展的基石. 要系统地、科学地建立和发展一套完整的理论体系, 就需要对基本原理进行提炼、抽象和升华, 使得工程控制的实践能够更加系统,并不断进入更高的层次, 从而“下学而上达”。

从PID到ADRC

积分控制器

三种矫正网络

超前校正网络 滞后矫正网络 超前-滞后矫正网络
这些都要配合BODE图去确定频率指标 设计较为复古，较为原始。

wc剪切频率处的中频段宽度对闭环系统特性有至关重要的影响。

更进一步—PID控制器

1 极点配置方法调节PID参数
确定极点位置来对闭环系统的Kp Ki进行确定。

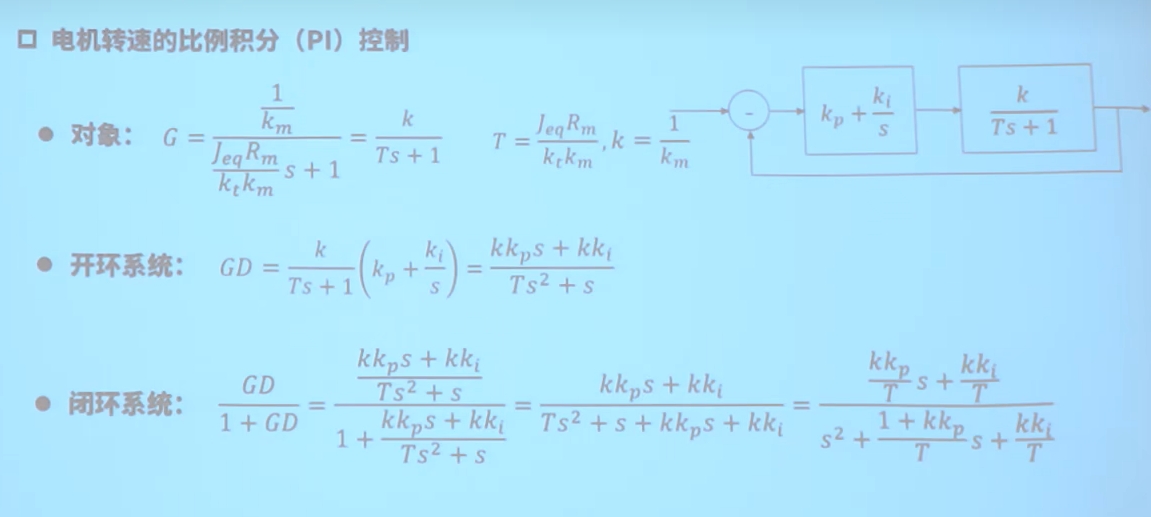
这里极点配置 根据一阶系统 二阶系统 的阶跃响应曲线来根据期望的TS调节时间根据经验选取。

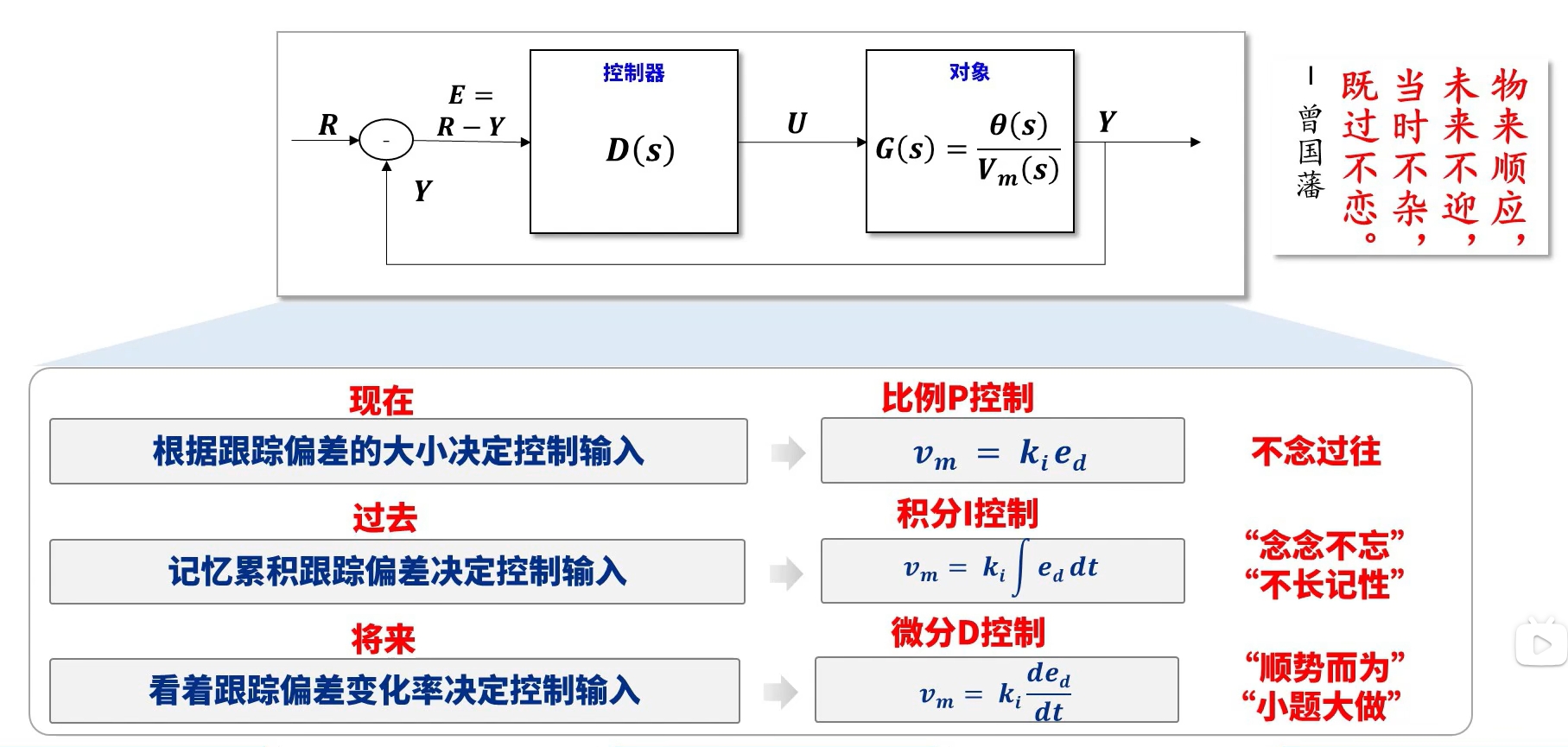
2 ZN方法调节PID参数

3 经验方法

积分串联型控制

简单理想发动机转速控制模型：

从扭矩 或者电压调整转速 这属于一阶系统。采用比例控制即可很好的进行控制 如下图所示设计控制过程。

从力矩到转速这属于积分环节：如下
$$ J\dot{\omega}=M $$
J是转动惯量，转速由w的导数表示。M为力矩。
则可以得到w与M的关系如下
$$ \frac{\omega}{M}=\frac{1}{Js} $$

设计如下：

简单理想发动机转角控制模型：

$$ \frac{\theta}{M}=\frac{1}{Js^2} $$
设计比例微分PD控制器。

现实世界中，几乎没有上述两种理想系统。
一阶系统有摩擦存在时，二阶系统有摩擦存在时，传统控制方法适用性不再好。
积分串联型真的好很容易控制，但是实际系统没有。我们ADRC需要构造这种系统。

误差积分被动补偿-创造理想系统

传统引入积分控制，便是提高了系统的型别。但是不一定会好用。

传统发动机控制电脑中，会有几千个PID参数表，用于对应不同的发动机工作环境。

总扰动的概念

扩张状态观测器ESO-估计总扰动

个人理解：扩张状态观测器，即在原本观测器的基础上，加入积分环节（一个积分环节对应一个状态，也就是直观的扩张出来了一个状态）。使得总扰动的估计能够消除稳态误差。
系统类似下图，使用Simulink模块简单画一下，表示一下

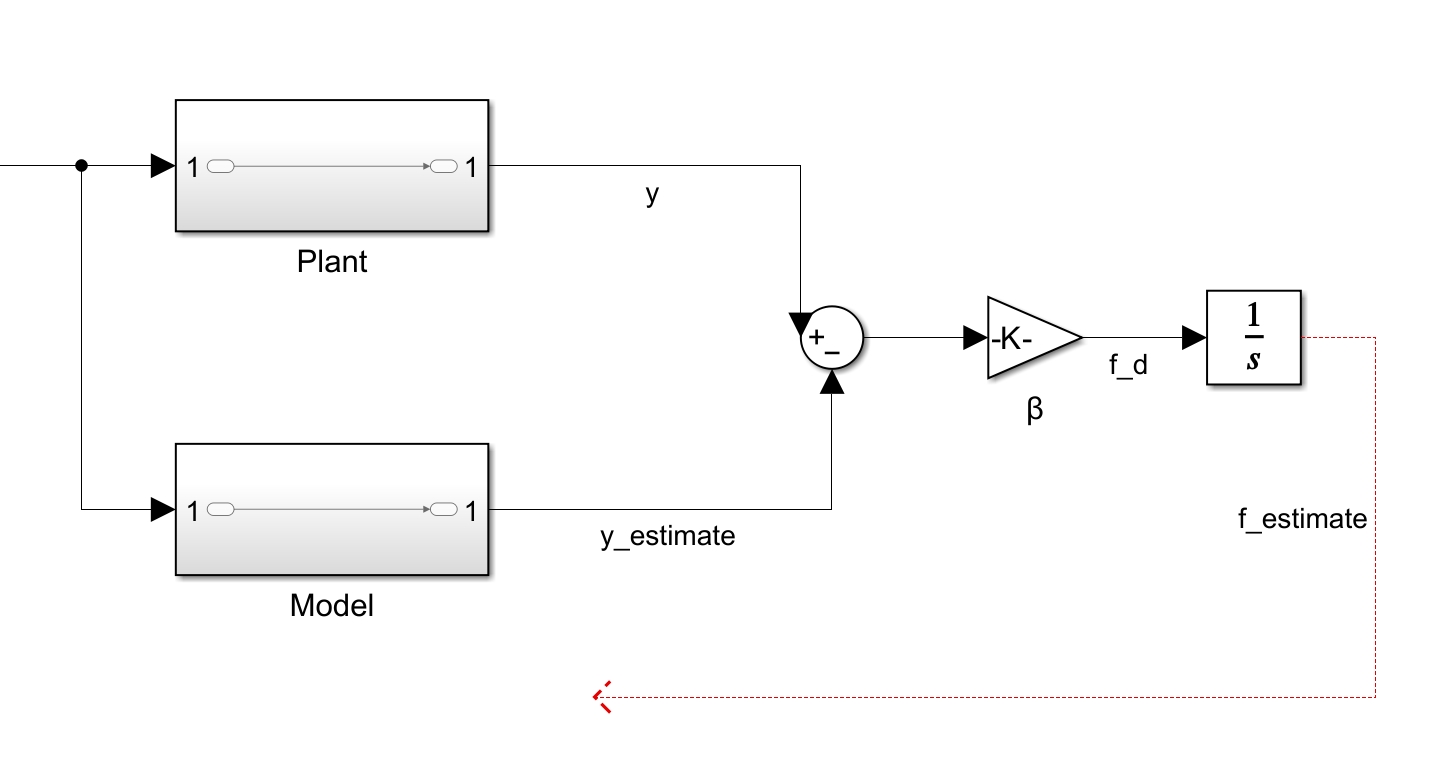
果然反步法的设计过程是重要的，这样看来也有一定相似之处。
观测器，观察每一个状态的演变过程，所以用导数。也就是状态方程。

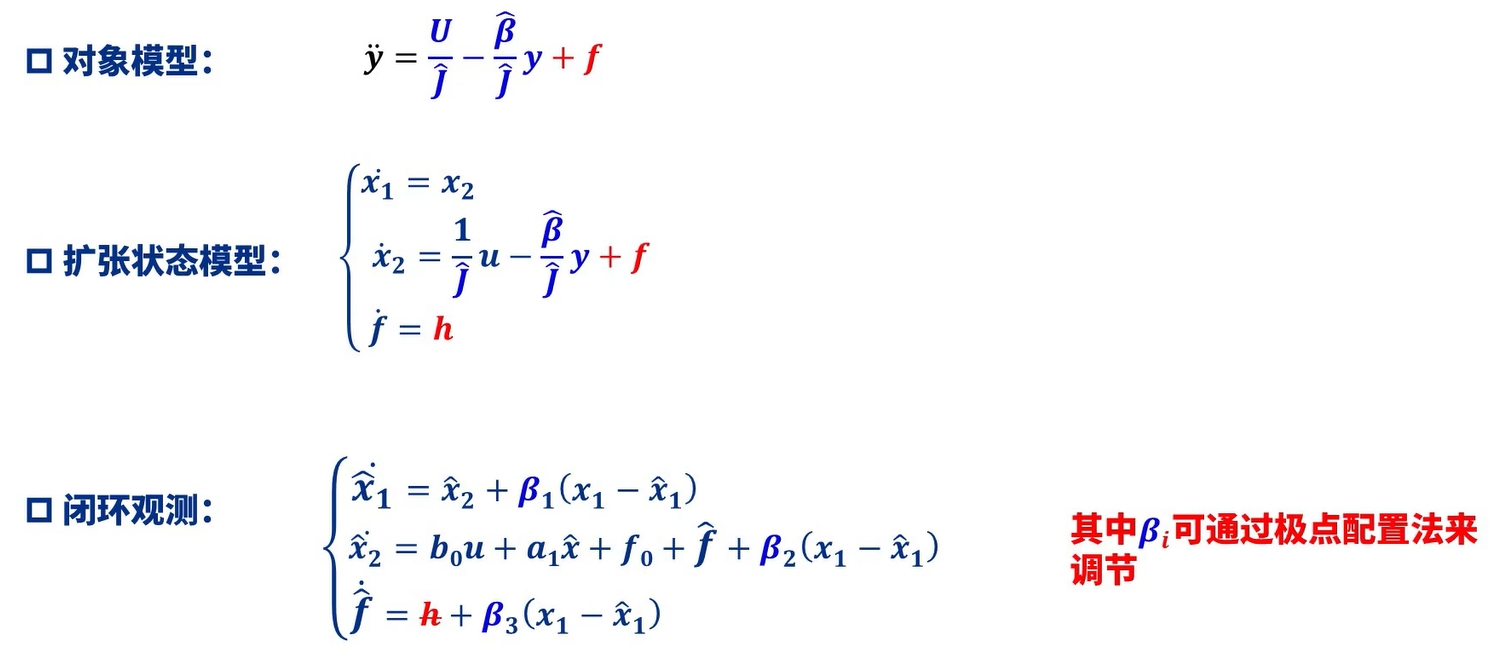
总扰动f的导不知道，先写一个h。
观测器使用测量的偏差与估计的偏差。分别矫正了所有状态的微分方程。只要参数β123调节好，就可以准确估计总扰动。便可以改造出积分串联型理想系统。进而可以很好的控制系统。

这样原本Y的二阶导只等于U0
此时U0采用比例微分控制即可实现完全控制。

扩张状态观测器ESO-如何选择β123？

对于
$$ \dot{y}=ay+bu $$
给定一个阶跃信号，决定系统调节速度的是a。
证明：写出传递函数如下：
$$ \frac{Y}{U}=\frac{b}{s+a} $$
a决定极点的位置。所以很明显决定系统稳定以及收敛速度的是a。
对状态空间表达式x导=Ax+bu也是如此。A决定系统稳定性以及各种性能。

特征值决定了状态空间中，每一个状态演变的快与慢。特征值也就是传递函数的极点。这是一个普遍且重要的理论。

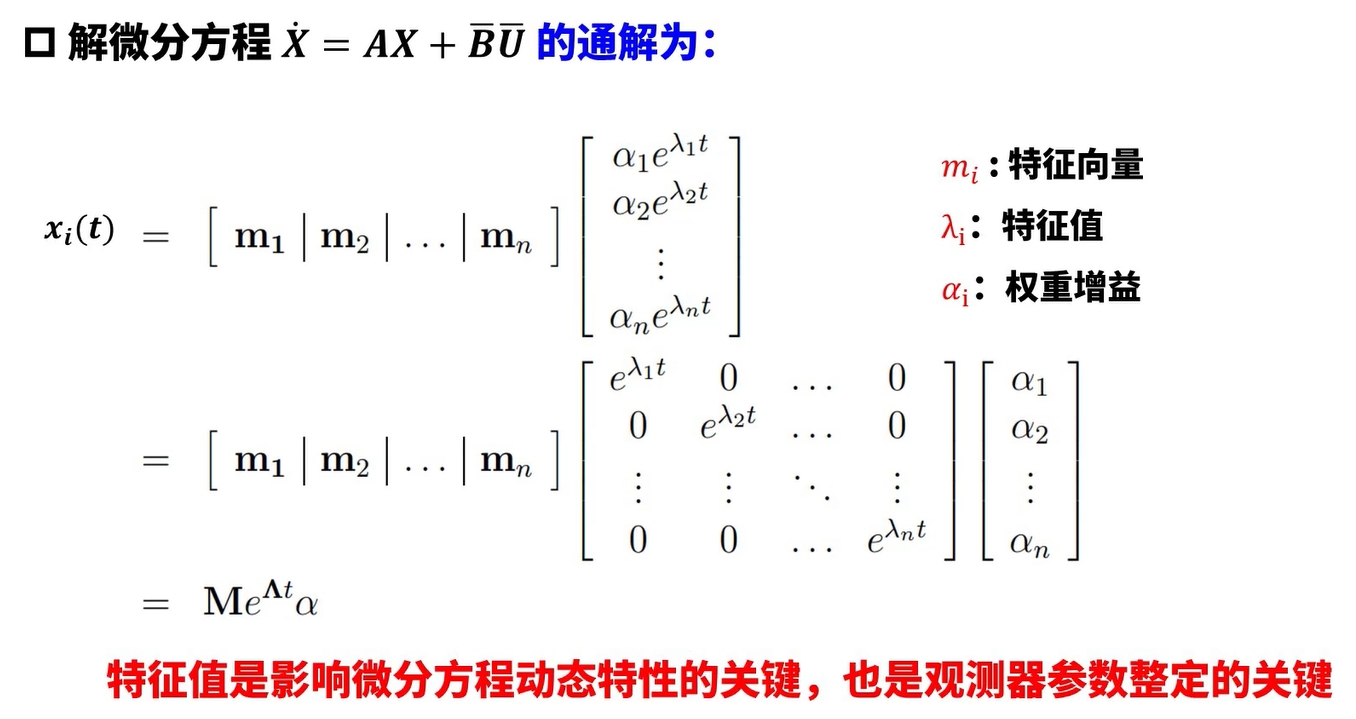
如何调整特征值？
A矩阵写出行列式$A-\lambda$。 令行列式等于0得到特征方程。 令特征方程等于
$$ \left( \lambda +\omega _0 \right) ^3=0 $$
对应相等即可求出β123。

ADRC中的fst函数

fst函数是ADRC跟踪微分器中的非线性控制器，负责计算加速度控制信号。
fst函数是非线性最速控制律（Fastest Control），它是ADRC中跟踪微分器（Tracking Differentiator, TD）里用于计算控制输入（类似“加速度”或“控制力”）的核心函数。
具体来说，fst函数根据当前的跟踪误差和速度，输出一个加速度控制信号，使得跟踪误差能够以最快速度收敛，同时保证系统的平滑性和鲁棒性。
一个经典ADRC控制中的FST函数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

function out = fst(x1, x2, omega, h)
%fst Summary of this function goes here
%   最速控制综合函数
d = omega * h;
d0 = x1 + h * d;
y = x1 + h * x2;
a0 = sqrt(d * d + 8 * omega * abs(y));
if abs(y) > d0
    a = x2 + (a0 - d) / 2 * sign(y);
else
    a = x2 + y / h;
end

if abs(a) > d
    out = - omega * sign(a);
else
    out = - omega * a / d;
end

end

x1：跟踪误差（这里是位置误差，即v1 - v0）
x2：当前速度（状态变量速度）
omega：设计参数，控制收敛速度的权重，类似“频率”
h：采样周期或滤波因子，影响控制平滑程度
输出 out 是加速度控制量，用于驱动跟踪误差快速收敛。
关键步骤说明：
参数计算
d = omega * h：一个阈值，用来区分控制策略
d0 = x1 + h * d 和 y = x1 + h * x2 是辅助计算量，用于判断当前误差状态

判断条件if abs(y) > d0 这是非线性分段条件，用于区分误差较大和较小时采用不同的控制策略。
当误差较大时（abs(y) > d0），采用一种非线性控制策略加快收敛。
当误差较小时，采用线性控制策略平滑收敛。

计算控制量a
计算一个加速度控制量a，根据误差和速度调整。
a越大，控制作用越强，推动误差快速减小。

输出控制信号out
根据a大小做饱和处理，保证输出在[-omega, omega]范围内，防止控制信号过大导致振荡。
输出out就是TD控制器对速度的“加速度控制”，用来驱动状态变量快速收敛。

ADRC中的fal函数

fal函数是ADRC控制器中常用的非线性函数（nonlinear function），它的全称是“fractional power function”或“非线性误差变换函数”。
它的主要作用是对误差e做一种平滑且带“非线性幂次”的变换，用于非线性反馈控制中，可以增强控制器对误差的响应速度和稳定性。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

function out = fal( e, a, delta )
%fal Summary of this function goes here
%   Detailed explanation goes here
if abs(e) > delta
    out = abs(e) ^ a * sign(e);
else
    out = e / (delta ^ (1 - a));
end

end

e：输入误差值，可以是位置误差、速度误差等。
a：幂次参数，通常0 < a < 1，控制非线性程度。
delta：临界阈值，用于定义分段非线性函数的范围。
分段说明： 当误差较大时：|e| > delta
使用非线性幂次函数 |e|^a * sign(e)。
这会使误差响应不是线性增长，而是一个小于1次幂的曲线，
当a<1时，误差较大时输出增长较慢，防止控制量过大。
当误差较小时：|e| <= delta
使用线性函数 e / (delta^(1 - a))，保证函数在e=0附近光滑连续，
防止非线性函数在小误差时过于“死板”，保证控制器灵敏响应。
为什么要这样设计？ 平滑性：函数在e = ±delta处连续且可导，避免了控制器输出跳变。
非线性控制效果：非线性幂次a让控制器在大误差时减弱输出，避免过冲；在小误差时线性提高灵敏度，保证快速收敛。
鲁棒性提升：这种设计提高了控制器在面对非线性和扰动时的性能。

ADRC中的ESO

状态空间方程推导而来的ESO，这个没什么好说的？
ESO 是ADRC的核心模块之一，主要用来：
在线估计系统的状态变量和总扰动（包含内部未知动态和外部扰动）。
实时补偿系统扰动，提高控制系统的鲁棒性和抗扰动能力。
ESO的设计目标是让观测误差快速收敛，从而准确估计系统的状态和扰动。
四旋翼中的ESO，二阶。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

function [dz1,dz2,dz3] = fcn(u,e,z2, z3)
%#连续形式的扩张状态观测器(ESO)

%% 参数赋值
beta01_y = 30;     % 可调参数
beta02_y = 300;     % 可调参数
beta03_y = 1000;   % 可调参数
a1 = 0.75;         % 可调参数
a2 = 0.5;          % 可调参数
a3 = 0.25;         % 可调参数
delta = 0.006;     % 线性段的区间长度
b0_y = 0.06;       % 决定补偿强弱的“补偿因子”

dz1 = z2 - beta01_y * fal(e, a1, delta);
dz2 = z3 - beta02_y * fal(e, a2, delta) + b0_y * u;
dz3 = - beta03_y * fal(e, a3, delta);

输入
u：控制输入信号（控制器输出的控制量）
e：观测误差，通常是测量输出与估计输出的误差，e = z1 - y（这里y是系统输出，z1是估计的状态）
z2, z3：ESO内部状态变量，对应系统速度状态和扰动估计
输出
dz1, dz2, dz3：状态变量的导数，供积分器计算下一时刻状态估计值